威布尔分析在产品失效模式评估中的应用举例

在进行产品寿命试验时，为了尽可能减少试验时间，节约试验成本，往往会提高试验应力进行评估。这里有一个前置条件：即假设认为在提高应力时，产品的失效模式不变。但是否在提高试验应力时，产品还保持了相似的失效机理呢？

此时威布尔分析作为在电子、机电和机械产品中广泛应用的寿命分析模型，在应对单一应力变化时，可以从简单快速的从数据的角度，来很好的解析这一问题。具体实施方法为：将失效数据进行威布尔拟合，通过判定形状参数β是否趋同，来评估失效模式是否一致。

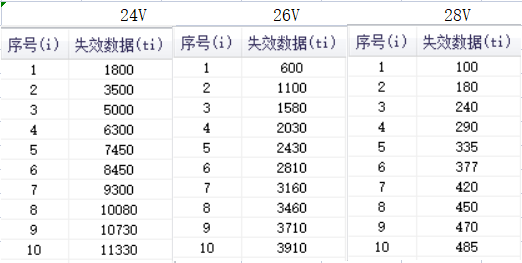
例程：某产品分别在供电电压24V、26V、28V时，各取10只进行试验，取得失效数据如截图所示，问其失效模式是否一致？

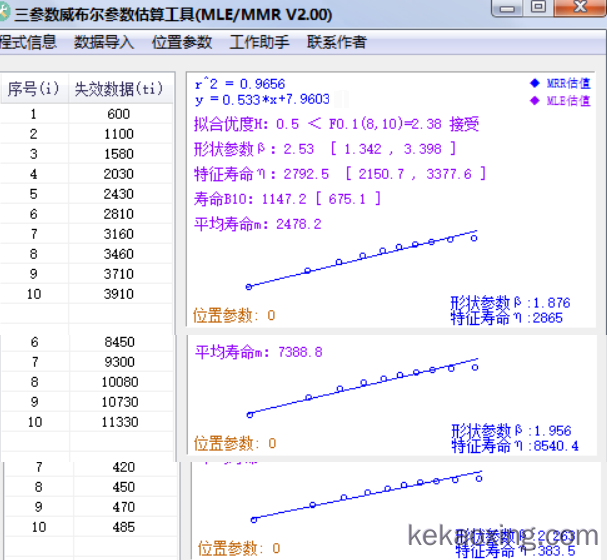
威布尔数据拟合数据如图所示，因中位秩法提供了拟合图，可以从图示数据的分布，形状参数1.876、1.956和2.263中表明：数据分布图和形状参数均非常接近，在3种电压条件下，产品的失效模式（失效机理）未发生变化，使用此电压加速方案是可行的。

此外，还可以通过特征寿命η，来拟合出电压加速曲线，获得不同电压下的经验加速因子（更为可靠的加速因子）。

在上述例程中，使用了两参数威布尔模型进行了拟合，如在拟合中发现拟合优度H拒绝接受威布尔分布，则可以尝试使用三参数威布尔参数估计的方法。 链接