前段时间有人推荐了一本振动冲击相关的中文书籍,大概看了下,里面提到了一个振动的加速模型,就是提高振动量级缩短试验时间,短时间内暴露潜在的疲劳应力失效;翻了一些资料,列出目前用的比较多的几个振动加速模型的公式~供大家参考讨论~
1. 先列出2个疲劳应力的振动加速模型:
1)T2/T1=(S1/S2)^m; 如下第一张截图,参考MIL-STD-810H;
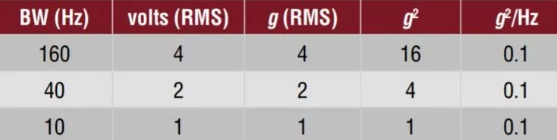
2)T2/T1=(Wf1/Wf2)^(m/2);如下第二张截图;参考MIL-STD-810H;
各参数意义如下:
T2—-等效测试时间;
T1—-指实际应用时振动时间;
S1—-加速测试时振动应力rms值;
S2—-实际应用时振动应力rms值;
Wf1—-ASD基于g2/HZ对应的加速测试时振动应力值;
Wf2—-ASD基于g2/HZ对应的实际应用时振动应力值;
其实上面两个公式是一个意思,对于正弦振动只用到第一个公式,对于随机振动,因为表述不同,参考下面截图就很容易看懂了,通常我们写随机振动时只会给两列,一列写一个Hz区间和对应值,一列写一个g2/Hz的对应值,其实也可以分解写成如下截图的样子,只是多了一个平方,所以第二个公式的幂为m/2;
m—-注意不同材料有不同的参考值;同时对于不同振动类型,随机与正弦振动,不同标准也给出了不同的参考值;简单罗列如下:
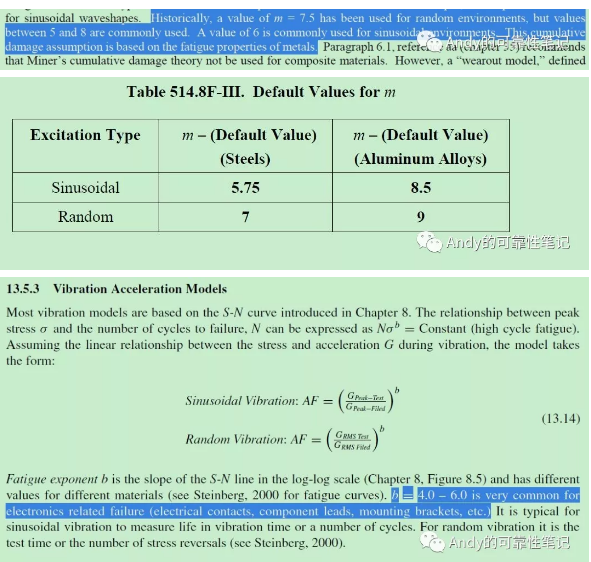
I:MIL-STD-810H中基于金属疲劳应力,通常对于随机振动m=7.5 ,但是通常5~8为常用值;对于正弦振动通常取值为m=6; 如下第1张截图;
II:依旧是MIL-STD-810H,对于钢和铝合金的m值,随机正弦给出了不同的参考值,如下第2张截图;
III:实用可靠性工程手册,给出了电子设备m的参考值,4~6;如下第3张截图;
IV:振动冲击手册第五版,给出了一个电子设备的通用参考值m=4;如下第4张截图;截图里的b就是m,只是不同标准写法不同而已;
V:NASA-HDBK-7005同样给出电子设备参考值m=4;如下第5张截图,依旧这里的截图里采用的b等同于m;
备注:如果有条件的话,实际的m精确值需要根据实验得出,如上值为不同的标准参考,但是通常公司都没有这个条件,如果不是单纯测试金属疲劳应力的话,对于电子设备振动疲劳应力,个人觉得可以参考NASA和振动冲击手册中的经验总结,取值m=4;
2. 包装运输振动加速模型:
这个是在查找上面疲劳应力振动加速资料时找到的,之前Mosch的公众号“摩西的可靠不可靠”也提过这个公式;这里也罗列一些资料供大家参考讨论~
包装振动加速压缩时间公式如下,这个公式起初来源没有找到,只是很多人在ISTA和ASTM会议中提出,参考如下第一张截图
IT = I0 *(T0 / TT)^(1/2) —-打不出来根号,用幂1/2表示下….;
IT—-加速振动测试的Grms值;
I0—-实际运输振动的Grms值;
T0—-实际运输时间;
TT—-实验室测试时间;
备注:这里建议T0 / TT的比例不大于5;也就是说实际运输时间假设为10小时,实验室测试时间建议至少2小时以上,这样去算实验室的加速振动值,其实这个公式换算过来就是上面的疲劳应力的m值取2;只不过这里首先限定了加速倍数;
例如假设实际运输时间15小时,实际振动Grms为0.245,假设取时间压缩比例5,则实验室振动测试Grms为0.245*[5^(1/2)]=0.548; 如下第3张截图;
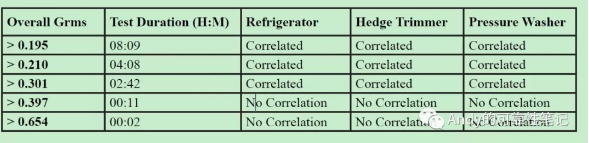
这里查到了一份Kyle Dunno曾经发表的一篇文章,截图如下,里面提到了一些具体的实际测试来验证加速试验时间倍数的可取性,他选用了三种产品做测试,先侦测实际运输Grms大概为0.195,记录下实际外场测试的失效现象;接着在实验室振动台用加速测试方法,观察测试后三种产品的失效现象是否与外场测试失效一致;结果发现当加速2.4倍压缩时间(0.301Grms)之前的一致性都很好,但是超过4倍(0.397)后三种产品测试失效与实际失效不一致;注意文章中主要还提到了涂层的失效,猜想这可能是为什么包装振动的加速倍数会比金属疲劳加速倍数低的一个原因;
文章链接如下:https://pdfs.semanticscholar.org/0f69/191505e3b8dca0d1402df60cd29c0f6a3bcb.pdf
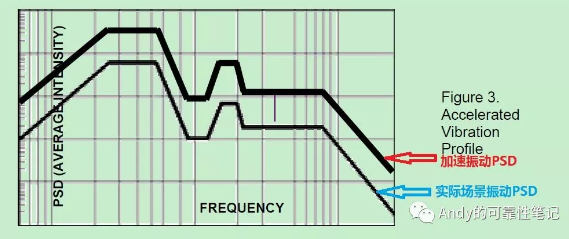
注意:如上提到的所有振动加速模型均要保持振动频谱图形不变(PSD整体向上平移);如下截图
总结:振动加速模型目前看来均符合逆幂律模型,如果没有实际的试验数据统计,具体的幂值m取值可参考文中提到的标准参考值~
个人水平有限,难免疏漏,如有错误和不同的观点欢迎交流指正~~
Andy的可靠性笔记 7月13日


















请登录之后再进行评论