印刷电路板组件的焊接点可能会因为温度循环作用导致疲劳失效。 Norris-Landzberg模型适用于分析焊点在器件重复开关过程中由温度循环作用引起的疲劳失效。
通过General log-linear (GLL)模型分析加速寿命数据,并进行参数变换可对应求出 Norris-Landzberg 模型的参数。
Norris-Landzberg 模型
模型中的失效循环数表达式为:
其中:
Nf 失效时的循环数
C 是一个系数
f 为循环频率 (循环/天)
ΔT 一个循环中的温度变化范围 (K)
Tmax 每个循环中的最高温度值 (K)
Ea 激活能 (eV)
K 为波兹曼常数 (8.617 x 10-5 eV/K)
m 和 n 为模型参数
模型描述了3种应力同时作用下焊点的寿命(低周期疲劳), Nf :
循环频率, f 满足逆幂律(IPL),
温度范围, ∆T 满足逆幂律(IPL),
最高温度, Tmax 满足 Arrhenius 寿命-应力关系.
加速因子 (AF), 实际应力下的寿命 (Nf,use) 与加速应力下寿命 (Nf,acc)的比值, 可表示为:
General Log-Linear 模型
在 general log-linear (GLL) 模型中, 特征寿命 L 与3个应力的关系如下:
特征寿命 L 可以用指定寿命分布中的百分位数表示。 它可以是Weibull分布的尺度参数eta,对数正态分布的中位数等。
为与Norris-Landzberg模型相对应,对 f 和 ΔT进行对数变换,并取Tmax的倒数
X1=ln(f),
X2=ln(∆T)
X3=1/Tmax, 得到,
将上式与Norris-Landzberg模型的等式进行比较, 可推出各参数的对应关系:
C = eα0
m = -α1
n = -α2
Ea/K =α3
以下是一个使用了3种应力且满足GLL寿命-应力关系的加速寿命测试,测试对象为某类型无铅焊点。 图表展示了温度循环测试的结果和不同应力水平的设置。 对于3应力模型,测试需要最少4组不同应力组合(有4个待求参数)。 假设每个应力组合使用10个样品测试。每百次循环查看样品。
图1, 4个热循环应力试验结果及相应的应力水平设置
假定样品的寿命数据服从对数正态分布。选择Inverse Power Law(IPL)作为 f (循环频率)和 ∆T(循环中温度的变化幅度)的应力模型,Tmax的 应力模型设为Arrhenius:
图2, 计算GLL模型参数
分析结果可用于计算Norris-Landzberg模型参数:
C = eα0 = 56,387
m = -α1 = 0.2955
n = -α2 = 1.789
Ea/K = α3 = 1419
因此,加速因子为:
使用AF推算出实际使用条件下的相关指标例如进行以下测试:
若测试数据得到焊点的平均寿命为1500(次循环)。
根据上述公式,
在实际应力下的预期平均寿命为 1500 x 8.79 = 13,185 次循环
参考资料
K. C. Norris and A. H. Landzberg, “Reliability of controlled collapse interconnections,” IBM Journal of Research and Development 13, no. 3 (1969): 266–271.
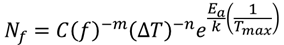























请登录之后再进行评论